数字信号处理(DSP)可以分为两类:固定点和浮点。
关于两个对应方的讨论和信息很多,但许多人在理解他们的差异以及这些差异如何影响现实世界的产品时仍然感到困惑。 本文的主要目的不是在技术上过深,而是以简单而直观的方式探索数字表示的差异。 由于将苹果与另一个苹果进行比较是公平的,因此我们将在本文中对两种符号使用相同的32位长度,如图1(下图)所示。
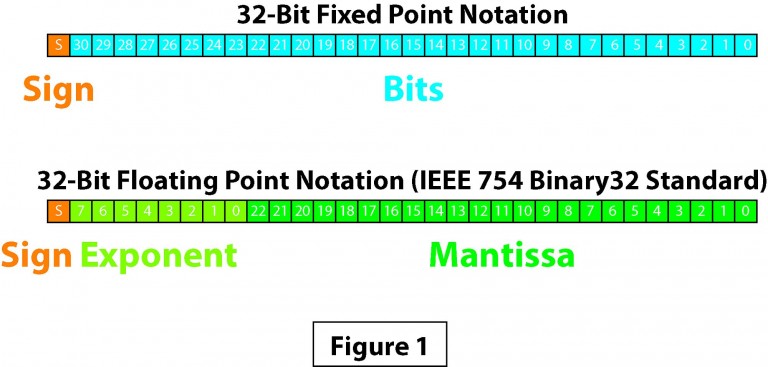
对于固定点表示法:
整数值= -1Sign x Bits
符号= 0(正值)或1(负值)
比特= 231个可能的值
正面最小值:1
正极限:+2147483647
通过简单的缩放,也可以表示小数。 所表示的值在整个范围内等间隔。 相邻值之间的间隙始终相同。
对于32位浮点(IEEE 754):
值= -1Sign x [(1+ Mantissa)x 2(Exponent-127)]
符号= 0(正值)或1(负值)
指数= 1到254(0和255保留用于特殊情况)。 减去127给出-126到127
对于所有’1’,所有’0’的尾数= 0到0.999999881。 添加1给出1.000000000到1.999999881
正极最小值:1 x2-126≈1.2×10-38
正极限:1.99999881 x2127≈3.4×1038
所表示的值在这两个极端之间是不等间隔的,使得相邻数字之间的间隙对于小值而言要小得多并且对于大数值而言要大得多。 这种符号“窃取”8位成为指数,这给出了广泛的动态范围,但为了获得这种好处,它失去了所有值的“被盗”8位分辨率。

图2(上图)说明了两种符号在数字表示方面的不同之处。 在此图中,我们只关注正数(符号位= 0)以避免并发症。 然后,标准定点格式中的八个最高有效位用作缩放索引,以匹配浮点格式中指数的位数。 这使得两种格式的剩余23位匹配。 完成位匹配后,我们就可以生成有意义的结果。
指数e可以是任意数字,只要所有块都在最小/最大范围(-126到127)之内。 一旦为固定点计算选择了所需的数据范围,Index = 1就映射到e。 该图表显示两个符号在i = 1时具有相同的23位分辨率。 对于i = 0,浮点的分辨率更好; 事实上,非常好。 有e + 126个浮点块,而只有一个固定点块(i = 0),两者都覆盖相同的数值范围。
对于1 <i <256,定点的分辨率更好。 虽然看起来浮点在较高值时会丢失,但请记住,固定点对应物总共只能有256(28)个块,每个块的分辨率为23位。 一旦该值超出上限,开发人员就被迫进一步扩大规模并以较低的分辨率生活,以便能够执行指定的数学任务。 这就是为什么浮点在计算值较小时占主导地位,并且在固定点不能处理时可以处理大数。 为了使定点DSP开发人员更加复杂,他们还必须处理溢出和截断错误。
总结:
浮点的优势:
- 动态范围极大
- 密集计算的应用程序
- 数字越小,精度越高,量化噪声越低
- 超出固定点能力的大数的可能计算
- 更简单,更快速的开发,无需担心溢出和截断错误
定点的优势:
- 在1 <i <256的窄范围内获得更好的分辨率(256个浮点指数块中的7个)
- 更简单的DSP芯片
Xilica处理器是40位浮点数。
Donny Chow是Xilica的创始人兼总工程师。 Xilica遵循Passion Through Performance的座右铭,为现场和安装的声音应用制造了领先的网络和独立DSP。

